A. BARISAN GEOMETRI
Barisan geometri adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan. Perbandingan atau rasio antara nilai suku-suku yang berdekatan selalu sama yaitu r. Nilai suku pertama dilambangkan dengan a.
Untuk mengetahui nilai suku ke-n dari suatu barisan geometri dapat dihitung dengan rumus berikut.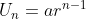
Barisan geometri adalah baris yang nilai setiap sukunya didapatkan dari suku sebelumnya melalui perkalian dengan suatu bilangan. Perbandingan atau rasio antara nilai suku-suku yang berdekatan selalu sama yaitu r. Nilai suku pertama dilambangkan dengan a.
Untuk mengetahui nilai suku ke-n dari suatu barisan geometri dapat dihitung dengan rumus berikut.
B. DERET GEOMETRI
Deret geometri adalah penjumlahan suku-suku dari barisan geometri.
Penjumlahan dari suku-suku pertama sampai suku ke-n barisan geometri dapat dihitung dengan rumus berikut.
Deret geometri adalah penjumlahan suku-suku dari barisan geometri.
Penjumlahan dari suku-suku pertama sampai suku ke-n barisan geometri dapat dihitung dengan rumus berikut.
dengan syarat r < 1
atau
dengan syarat r > 1
C. CONTOH SOAL BARISAN DAN DERET GEOMETRI
Soal no 1
Diketahui suku ke-5 dari barisan geometri adalah 243, hasil bagi suku ke-9 dengan suku ke-6 adalah 27. Suku ke-2 dari barisan tersebut adalah …
Pembahasan:
Diketahui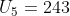
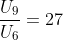
Ditanya
Jawab:
Sebelum kita mencari nilai dari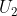 , kita akan mencari nilai a dan r terlebih dahulu.
, kita akan mencari nilai a dan r terlebih dahulu.
Ingat kembali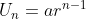 maka
maka
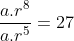

![r=\sqrt[3]{27}](https://latex.codecogs.com/gif.latex?r=\sqrt[3]{27})
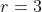
Substitusikan r = 3 ke persamaan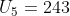
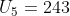
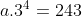

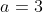
sehingga
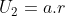
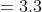
= 9
Jadi, suku ke-2 dari barisan tersebut adalah 9.
Diketahui
Ditanya
Jawab:
Sebelum kita mencari nilai dari
Ingat kembali
Substitusikan r = 3 ke persamaan
sehingga
= 9
Jadi, suku ke-2 dari barisan tersebut adalah 9.
Soal no 2
Selembar kertas dipotong menjadi dua bagian. Setiap bagian dipotong menjadi dua dan seterusnya. Jumlah potongan kertas setelah potongan kelima sama dengan …
Pembahasan:
Diketahui: a = 1
r = 2
Ditanya:
Jawab:


=32
Jadi, jumlah potongan kertas setelah potongan kelima adalah 32
Diketahui: a = 1
r = 2
Ditanya:
Jawab:
=32
Jadi, jumlah potongan kertas setelah potongan kelima adalah 32
Soal no 3
Diketahui suku ke-2 dan ke-4 barisan geometri berturut-turut adalah 12 dan 27. Jika nilai r > 0, tentukan nilai dari suku ke-3!
Pembahasan:
Diketahui:
U2 = 12
U4 = 27
r > 0
Ditanya: U3 =…?
Pembahasan:
Nyatakan suku ke-2 dan ke-4 dalam notasi matematis. Lakukan pembagian antara kedua suku seperti berikut.
Lakukan pembagian antara kedua suku seperti berikut. Setelah rasio diketahui, tentukan suku ke-3nya.
Setelah rasio diketahui, tentukan suku ke-3nya. Jadi, nilai dari suku ke-3 adalah 18.
Jadi, nilai dari suku ke-3 adalah 18.
Diketahui:
U2 = 12
U4 = 27
r > 0
Ditanya: U3 =…?
Pembahasan:
Nyatakan suku ke-2 dan ke-4 dalam notasi matematis.
 Lakukan pembagian antara kedua suku seperti berikut.
Lakukan pembagian antara kedua suku seperti berikut. Setelah rasio diketahui, tentukan suku ke-3nya.
Setelah rasio diketahui, tentukan suku ke-3nya. Jadi, nilai dari suku ke-3 adalah 18.
Jadi, nilai dari suku ke-3 adalah 18.Soal no 4
Pada sebuah deret geometri diketahui bahwa suku pertamanya adalah 3 dan suku ke-9 adalah 768. Suku ke-7 deret tersebut adalah …
Pembahasan :
Diketahui: a = 3
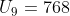
Ditanya:
Jawab:
Sebelum kita mencari nilai dari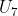 , kita akan mencari nilai r terlebih dahulu.
, kita akan mencari nilai r terlebih dahulu.
Ingat kembali bahwa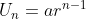 sehingga
sehingga  dapat ditulis menjadi
dapat ditulis menjadi
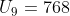
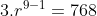
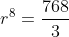

![r=\sqrt[8]{256}](https://latex.codecogs.com/gif.latex?r=\sqrt[8]{256})
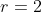
𝑆ehingga,

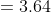

Jadi, suku ke-7 deret tersebut adalah 192.
Diketahui: a = 3
Ditanya:
Jawab:
Sebelum kita mencari nilai dari
Ingat kembali bahwa
𝑆ehingga,
Jadi, suku ke-7 deret tersebut adalah 192.
Soal no 5
Kamu berinvestasi sebesar Rp10.000.000. Pada bulan pertama kamu investasi, keuntungan yang diperoleh adalah Rp2.000. Pada bulan kedua, keuntungannya menjadi Rp4.000 dan bulan ketiga menjadi Rp8.000. Kira-kira berapa keuntungan yang kamu dapatkan setelah 10 bulan berinvestasi? Dan berapa total uang yang bisa kamu kumpulkan setelah berinvestasi selama 10 bulan?
Pembahasan:
Pada kondisi tersebut, keuntungan setiap bulan merupakan kelipatan 2 dari bulan sebelumnya. Artinya, jika dibentuk barisan, keuntungan tersebut akan menjadi barisan geometri, yaitu Rp2.000, Rp4.000, Rp8.000, …,Un. Setelah 10 bulan, keuntungannya akan menjadi:

Jadi, keuntungan yang akan kamu dapatkan setelah berinvestasi selama 10 bulan adalah Rp2.046.000 dengan total uang mencapai Rp10.000.000 + Rp2.046.000 = Rp12.046.000.

Tidak ada komentar:
Posting Komentar