MATRIKS

 PENGERTIAN MATRIKS

     Dalam matematika, matriks adalah susunan bilangan, simbol, atau ekspresi yang disusun dalam baris dan kolom sehingga membentuk suatu bangun persegi. Sebagai contoh, dimensi matriks di bawah ini adalah 2 × 3 karena terdiri dari dua baris dan tiga kolom:

 

jika dua matriks memiliki ukuran yang sama (masing-masing matriks memiliki jumlah baris dan jumlah kolom yang sama), kedua matriks tersebut dapat dijumlahkan maupun dikurangkan secara elemen demi elemen. Namun, berdasarkan aturan perkalian matriks, dua matriks hanya dapat dikalikan jika jumlah kolom matriks pertama sama dengan jumlah baris matriks kedua (artinya, perkalian matriks (m×n) dengan matriks (n×p) menghasilkan matriks (m×p)). Perkalian matriks tidak bersifat komutatif

 

Setiap objek dalam matriks ${\displaystyle {\boldsymbol {A}}}$ ukuran ${\displaystyle m\times n}$ sering dilambangkan dengan ${\displaystyle a_{i,j}}$, dimana nilai maksimum ${\displaystyle i=m}$ dan nilai maksimum ${\displaystyle j=n}$. Objek dalam matriks disebut elemen, entri, atau anggota matriks

 

MACAM-MACAM MATRIKS 

Ada beberapa jenis jenis matriks dalam matematika yang perlu diketahui, termasuk matriks kolom, matriks baris, matriks persegi, matriks diagonal, matriks identitas, matriks skalar, matriks nol, matriks transpose, dan matriks simetri. Berikut ini penjelasan jenis-jenis matriks.

Matriks kolom

Ini adalah matriks yang hanya memiliki satu kolom. Secara umum matriks kolom berordo m x 1 dapat dinotasikan sebagai  A=[a_ij]m×1

Matriks baris

Ini adalah matriks yang hanya memiliki satu baris. Secara umum matriks baris berordo 1 x n dapat dinotasikan sebagai  B=[b_ij]1×n.

Matriks persegi

Ini adalah matriks yang memiliki banyak baris dan kolom yang sama. Secara umum matriks persegi berordo m x m dapat dinotasikan sebagai A =  [a_ij]m×m

Matriks diagonal

Ini adalah matriks persegi yang semua elemen-elemennya bernilai nol kecuali elemen diagonal utama. Matriks B = [b_ij]m×n dikatakan matriks diagonal jika  b_ij =0 untuk  i≠j.

Matriks Identitas

Ini adalah matriks diagonal yang semua elemen diagonal utamanya bernilai 1. Matriks identitas dengan ordo n x n ditulis I_n.

Matriks Skalar

Ini adalah matriks hasil kali antara suatu skalar dengan matriks identitas. Elemen-elemen dalam diagonal utama bernilai sama dengan skalar.

Matriks Nol

Ini adalah semua matriks yang elemennya bernilai nol. Matriks nol dinotasikan dengan O.

Matriks Transpose

Ini adalah matriks yang diperoleh dengan cara mengubah baris matriks menjadi kolom matriks. Matriks Transpose dilambangkan dengan A^T atau A’.

Matriks Simetri

Matriks persegi A = [a_ij] disebut matriks simetris, jika A^T = A atau a_ji = a_ij untuk semua i, j.

 

OPERASI HITUNG MATRIKS 

Penjumlahan Matriks

Operasi hitung matriks pada penjumlahan memiliki syarat yang harus dipenuhi agar dua buah matriks dapay dijumlahkan. Syarat dari dua buah matriks atau lebih dapat dijumlahkan jika memiliki nilai ordo yang sama. Artinya, semua matriks yang dijumlahkan harus memiliki jumlah baris dan kolom yang sama.

Matriks dengan jumlah baris 3 dan kolom 4 hanya bisa dijumlahkan dengan matriks dengan jumlah baris 3 dan kolom 4. Matriks dengan jumlah baris 3 dan kolom 4 tidak bisa dijumlahkan dengan matriks dengan jumlah baris 4 dan kolom 3. Kesimpulannya, jumlah baris dan kolom antar dua matriks yang akan dijumlahkan harus sama.

Operasi hitung penjumlahan matriks memenuhi sifat komutatif, asosiatif, memiliki matriks identitas matriks nol, dan memiliki lawan matriks. Lawan matriks A adalah matriks , di mana elemen-elemen matriks merupakan lawan dari elemen-elemen matriks A. Secara ringkas, sifat operasi penjumlahan matriks dapat dilihat pada gambar di bawah.

Selanjutnya, kita akan mempelajari cara melakukan operasi hitung penjumlahan dua buah matriks. Penjelasan akan diberikan dalam bentuk contoh soal secara umum.

Contoh cara melakukan operasi penjumlahan pada matriks:

 

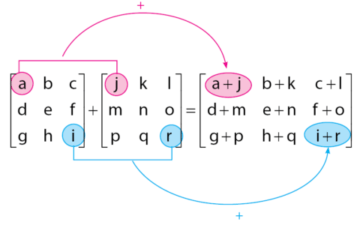
Bagaimana penjelasan mengenai penjumlahan matriks, mudah bukan? Sekarang kita akan masuk pada pembahasan selanjutnya yaitu operasi hitung pengurangan matriks. Simak uraian di bawah.

 

Pengurangan Matriks

Seperti halnya operasi hitung penjumlahan matriks, syarat agar dapat mengurangkan elemen-elemen antar matriks adalah matriks harus memiliki nilai ordo yang sama. Cara melakukan operasi pengurangan pada matriks dapat dilihat seperti cara di bawah.

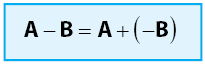
Cara melakukan operasi pengurangan dua matriks tidak jauh berbeda dengan penjumlahan matriks. Untuk lebih jelasnya, perhatikan contoh soal pengurangan matriks secara umum yang akan diberikan di bawah.

Contoh cara melakukan operasi pengurangan pada matriks:

 

 
 

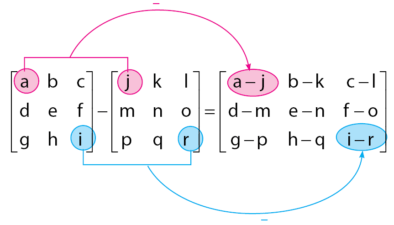
Perkalian Matriks

Pembahasan operasi hitung matriks selanjutnya yang akan dibahas adalah perkalian matriks. Perkalian matriks yang akan dibahas di bawah adalah perkalian matriks dengan skalar dan perkalian matriks dengan matriks. Selengkapnya simak operasi hitung perkalian matriks di bawah.

Perkalian Matriks dengan Skalar

Cara melakukan operasi skalar pada matriks adalah dengan mengalikan semua elemen-elemen matriks dengan skalarnya. Jika k adalah suatu konstanta dan A adalah matriks, maka cara melakukan operasi perkalian skalar dapat dilihat melalui cara di bawah.

 

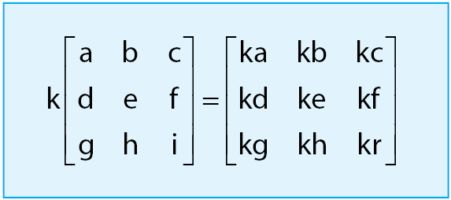
Cara melakukan perkalian matriks dengan skalar cukup mudah dilakukan. Contoh soal cara melakukan perkalian matriks yang akan diberikan di bawah akan menambah pemahaman sobat idschool.

Contoh cara melakukan operasi perkalian skalar pada matriks:

Diketahui konstanta k = 2 dan sebuah matriks A dengan persamaan seperti di bawah.

   

Maka hasil perkalian konstanta k dengan matriks A adalah sebagai berikut.

   

   

 

Uraian selanjutnya adalah cara melakukan perkalian dua matriks.

 Operasi Perkalian Dua Matriks

Seperti yang telah disinggung sebelumnya, syarat dua buah matriks dapat dikalikan jika memiliki jumlah kolom matriks pertama yang sama dengan jumlah baris matriks ke dua. Ordo matriks hasil perkalian dua matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.

Matriks A memiliki jumlah kolom sebanyak m dan jumlah baris r, matriks B memiliki jumlah kolom sebanyak r dan jumlah baris m, hasil perkalian matriks A dan B adalah matriks C dengan jumlah kolom m dan jumlah baris n.

 

 

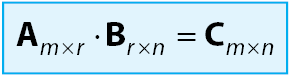
Sebelum mengulas cara melakukan operasi perkalian dua buah matriks, sebaiknya kita perlajari dahulu sidat-sifat operasi perkalian dua matriks. Sifat-sifat operasi perkalian matriks meliputi sifat asosiatif, distributif, dan memiliki matriks identitas I. Sifat-sifat operasi perkalian matriks dapat dilihat pada gambar di bawah.

Sifat-sifat matriks di atas dapat digunakan untuk memudahkan perhitungan dalam melakukan operasi hitung matriks.

Sekarang, pembahasan kita masuk pada perkalian dua matriks. Untuk pembahasan pertama kita akan mempelajari cara melakukan perkalian matriks dengan ukuran 2 2 dan matriks dengan ukuran 2 1.

 

Proses cara melakukan operasi perkalian matriksdengan ukuran 2 2 dan matriks dengan ukuran 2 1 dapat disimak pada pembahasan di bawah.

Diketahui:

   

   

 
Perkalian dua matriks dapat diperoleh dengan cara di bawah.
 

 

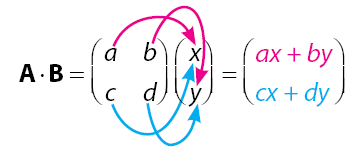
Selanjutnya adalah perkalian dua matriks. Kedua matriks yang akan dioperasikan sama-sama berukuran 2 2. Selengkapnya, simak pembahasan di bawah.

Diketahui:

   

   

 
Maka perkalian dua matriks dapat diperoleh dengan cara di bawah.
 

 

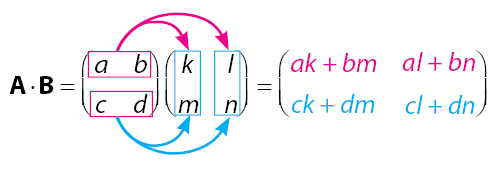
Untuk lebih jelasnya akan ditunjukkan dari contoh soal operasi perkalian dua matriks seperti yang ditunjukkan di bawah.

Diketahui:

   

   

Maka:

   

   

   

  

 CONTOH SOAL MATRIKS

Contoh Soal 1

Jika diketahui persamaan metrik !

A. 4
B. 5
C. 7
D. 29
E. 31

Pembahasannya :

Karena kedua matriks sama, maka elemen-elemen yang seletak akan sama pula, sehingga berlaku:

2x + 1 = 3
2x = 2
x = 1
y + 12 = 15
y = 3
x + y = 1 + 3 = 4

Jadi Jawabanya adalah : 4 (a)

Contoh Soal 2

 Contoh Soal 3

 

Contoh Soal 4

Jika determinan nilai matriks A adalah 4 kali determinan nilai matriks B, maka nilai x adalah…

 A. 4/3 
B. 8/3 
C. 10/4 
D. 5/3 
E. 16/7

Pembahasannya:
det A = 4 det B 
4 ^x (16 ^x ) – (-16) = 4 (108 – (-152)) 
4 ^x (4 ^2x ) + 16 = 4 (260) 
4 ^3x = 4 (260) – 16 
4 ^3x = 4 (260) – 4 (4) 
4 ^3x = 4 (260 – 4) 
4 ^3x = 4 (256) 
4 ^3x = 4. 4 ⁴
4 ^3x = 4 ⁵
3x = 5 
x = 5/3

Jawabannya : D

 

Contoh Soal 5 

 

 

SC :

https://idschool.net/sma/operasi-hitung-penjumlahan-pengurangan-perkalian-matriks/

https://rumus.waheedbaly.com/contoh-soal-matriks-dan-jawabannya-kelas-11/

 

 

 

 

SOAL CERITA UNTUK MENENTUKAN NILAI OPTIMUM

 SOAL CERITA UNTUK MENENTUKAN NILAI OPTIMUM

Soal

“Dewi akan membuat 2 model pakaian jadi. Model I memerlukan tidak lebih dari 1 m kain polos dan 1,5 m kain bergaris. Model II memerlukan tidak lebih dari 2 m kain polos dan 0,5 m kain bergaris. Bila pakaian tersebut dijual, setiap model I memperoleh untung tidak kurang dari Rp. 15.000,00 dan model II memperoleh untung tidak kurang dari Rp. 10.000,00. Laba yang diperoleh Dewi adalah sebanyak ….” Buat Pertidaksamaannya dulu baru table setelah itu daerah kotor dan daerah bersihnya, himpunan penyelesaian, titik pojok untuk menentukan nilai optimalnya dan laba Dewi dari nilai tertinggi yang diperoleh?

Jawab :

Laba maksimal Rp 140.000 akan diperoleh jika memproduksi 4 baju model I dan 8 baju model II 

logika MATEMATIKA

 Halo Teman Teman Kali ini Saya Egha Ramdhani Akan Membahas Apa itu Logika Matematika

Logika matematika adalah cabang Logika dan Matematika yang mengandung kajian logika matematis dan aplikasi kajian ini pada bidang-bidang lain di luar matematika. Logika matematika berhubungan erat dengan Ilmu Komputer dan logika filosofis Tema utama dalam logika matematika antara lain adalah kekuatan ekspresif dari logika Formal dan kekuatan deduktif dari sistem Pembuktian formal. Logika matematika sering dibagi ke dalam cabang-cabang dari teori himpunan, teori model, teori rekursi,teori pembuktian serta matematika konstruktif. Bidang-bidang ini memiliki hasil dasar logika yang serupa.

Ada 13 Hukum logika yaitu :

1. Hukum komutatif
   • p ∧ q ≡ q ∧ p
   • p ∨ q ≡ q ∨ p
2. Hukum asosiatif
   • (p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
   • (p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
3. Hukum distributif
   • p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
   • p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
4. Hukum identitas
   • p ∧ B ≡ p
   • p ∨ S ≡ p
5. Hukum ikatan
   • p ∧ S ≡ S
   • p ∨ B ≡ B
6. Hukum negasi
   • p ∧ ~p ≡ S
   • p ∨ ~p ≡ B
7. Hukum negasi ganda
   • ~(~p) ≡ p
8. Hukum idempotent
   • p ∧ p ≡ p
   • p ∨ p ≡ p
9. Hukum De Morgan
   • ~(p ∧ q) ≡ ~p ∨ ~q
   • ~(p ∨ q) ≡ ~p ∧ ~q
10. Hukum penyerapan
    • p ∧ (p ∨ q) ≡ p
    • p ∨ (p ∧ q) ≡ p
11. Negasi B dan S
    • ~B ≡ S
    • ~S ≡ B
12. p → q ≡ ~p ∨ q
13. p ↔ q ≡ (~p ∨ q) ∧ (p ∨ ~q)

dan di dalam Logika Matematika terdapat yang namanya " Tabel Kebenaran "

Tabel kebenaran adalah tabel dalam Matematika yang digunakan untuk melihat nilai kebenaran dari suatu premis/pernyataan. Jika hasil akhir adalah benar semua (dilambangkan B, T, atau 1), maka disebut Tautologi. Sedangkan jika salah semua (S, F, atau 0) disebut Kontradiksi. Premis yang hasil akhirnya gabungan benar dan salah disebut kontingensi. 

Ada Beberapa Jenis Operasi pada tabel kebenaran Yaitu :

1. Negasi

Tabel kebenaran untuk TIDAK p (juga ditulis ¬p, Np, Fpq, or ~p) adalah di bawah ini: 

Logika negasi 

p	¬p
B	S
S	B

1. Konjungsi

Tabel kebenaran untuk p DAN q (juga ditulis p ∧ q, Kpq, p & q, atau p  q) adalah di bawah ini: 

p	q	p ∧ q
B	B	B
B	S	S
S	B	S
S	S	S

1. Disjungsi inklusif (sering disebut sebagai disjungsi saja)

Tabel kebenaran untuk p ATAU q (juga ditulis p ∨ q, Apq, p || q, or p + q) adalah di bawah ini: 

Logika Disjungsi

p	q	p ∨ q
B	B	B
B	S	B
S	B	B
S	S	S

1. Implikasi

Tabel kebenaran untuk XN p (juga ditulis p → q, Cpq, p ⇒ q) adalah di bawah ini: 

Logika kesamaan

p	q	p ⇒ q
B	B	B
B	S	S
S	B	B
S	S	B

1. Kesamaan atau Bikondisional (sering disebut sebagai biimplikasi saja)

Tabel kebenaran untuk p XNOR q (juga ditulis p ↔ q, Epq, p = q, or p ≡ q) adalah di bawah ini: 

Logika kesamaan

p	q	p ≡ q
B	B	B
B	S	S
S	B	S
S	S	B

1. Disjungsi eksklusif

Tabel kebenaran untuk p XOR q (juga ditulis p ⊕ q, Jpq, or p ≠ q) adalah di bawah ini: 

Disjungsi eksklusif

p	q	p ⊕ q
B	B	S
B	S	B
S	B	B
S	S	S

dan Di logika Matematika ada yang namanya Invers,Konvers,dan Kontraposisi

• nvers dari  adalah ~p → ~q
• Konvers dari  adalah q → p
• Kontraposisi dari  adalah ~q → ~p

Ada cara penarikan Kesimpulan di logika matematika yaitu :

Modus ponens

premis 1: p → q

premis 2: p

kesimpulan: q

Modus tollens

premis 1: p → q

premis 2: ~q

kesimpulan: ~p

Silogisme

premis 1: p → q

premis 2: q → r

kesimpulan: p → r 

CONTOH Soal Logika Matematika

Soal No. 1
Tentukan pernyataan majemuk hasil penggabungan pasangan-pasangan pernyataan berikut dengan menggunakan operasi konjungsi (DAN):
a) p : Hari ini Jakarta hujan
    q : Hari ini Jakarta banjir

b) p : Iwan memakai topi
    q : Iwan memakai dasi

c) p : Mahesa  anak jenius.
    q : Mahesa anak pemalas.

Pembahasan
a) p : Hari ini Jakarta hujan
    q : Hari ini Jakarta banjir

p ∧ q : Hari ini Jakarta hujan dan banjir

b) p : Iwan memakai topi
    q : Iwan memakai dasi

p ∧ q : Iwan memakai topi dan dasi

c) p : Mahesa anak jenius.
    q : Mahesa anak pemalas.

p ∧ q : Mahesa anak jenius tetapi pemalas

Kata "dan"  bisa diganti dengan "tetapi", "walaupun", "meskipun" selaraskan dengan pernyataan.

Soal No. 2
Diberikan dua pernyataan sebagai berikut:
a) p : Hari ini Jakarta hujan lebat.
    q : Hari ini aliran listrik putus.

Nyatakan dengan kata-kata:
a) p ∧ q
b) p ∧ ~q
c) ~p ∧ q
d) ~p ∧ ~q

Pembahasan
a) Hari ini Jakarta hujan lebat dan aliran listrik putus
b) Hari ini Jakarta hujan lebat dan aliran listrik tidak putus
c) Hari ini Jakarta tidak hujan lebat dan aliran listrik putus
d) Hari ini Jakarta tidak hujan lebat dan aliran listrik tidak putus

Soal No. 3
Diberikan data:
Pernyataan p bernilai salah
Pernyataan q bernilai benar

Tentukan nilai kebenaran dari konjungsi di bawah ini:
a) p ∧ q
b) p ∧ ~q
c) ~p ∧ q
d) ~p ∧ ~q

Pembahasan
Tabel Nilai kebenaran untuk konjungsi :

p	q	p ∧ q
B	B	B
B	S	S
S	B	S
S	S	S

Terlihat bahwa konjungsi bernilai benar jika kedua pernyataan bernilai benar.
Kita terapkan pada soal salah satunya dengan cara tabel:

p	q	~p	~q	p ∧ q	p ∧ ~q	~p ∧ q	~p ∧ ~q
S	B	B	S	S	S	B	S

Dari tabel di atas
a) p ∧ q bernilai salah
b) p ∧ ~q bernilai salah
c) ~p ∧ q bernilai benar
d) ~p ∧ ~q bernilai salah

Soal No. 4
Tentukan negasi dari pernyataan-pernyataan berikut:

a) Hari ini Jakarta banjir.

b) Kambing bisa terbang.

c) Didi anak bodoh

d) Siswa-siswi SMANSA memakai baju batik pada hari Rabu.

Pembahasan
a) Tidak benar bahwa hari ini Jakarta banjir.
b) Tidak benar bahwa kambing bisa terbang.
c) Tidak benar bahwa Didi anak bodoh
d) Tidak benar bahwa siswa-siswi SMANSA memakai baju batik pada hari Rabu.

Atau boleh juga dengan format berikut:
a) Hari ini Jakarta tidak banjir.
b) Kambing tidak bisa terbang.
c) Didi bukan anak bodoh
d) Siswa-siswi SMANSA tidak memakai baju batik pada hari Rabu.

Soal No. 5
Tentukan negasi (ingkaran) dari pernyataan-pernyataan berikut:
a) p : Semua dokter memakai baju putih saat bekerja.
b) p : Semua jenis burung bisa terbang
c) p : Semua anak mengikuti ujian fisika hari ini.

Pembahasan
Pernyataan yang memuat kata "Semua" atau "Setiap" negasinya memuat kata "Beberapa" atau "Ada" seperti berikut:
a) ~p : Ada dokter tidak memakai baju putih saat bekerja.
b) ~p : Beberapa jenis burung tidak bisa terbang
c) ~p : Beberapa anak tidak mengikuti ujian fisika hari ini.

Sekian Dari Saya kurang lebihnya mohon maaf , Wassalamualaikum warahmatullahi wabarokatu

Daerah Bersih dan Daerah kotor ( Program linier)

 

 Gambar Daerah Bersih dan Daerah Kotor

 

SOAL

 

Gambar daerah bersih dan daerah kotor dari pertidaksamaan 3x + 2y ≤ 12, 5x + 3y < 19, x ≥ 0, y > 0

 

Pembahasan

 

• 3x + 2y ≤ 12

 x = 0

3.0 + 2y = 12

         2y = 12

           y = 6

3x + 2.0 = 12

         3x = 12

           x = 4

 

 

 

• 5x + 3y < 19

  y = 0

 5x + 3.0 = 19

          5x = 19

            x = 3,8

 5.0 + 3y = 19

          3y = 19

            y = 6,3

 

 

 

Daerah Penyelesaian

 

 

daerah penyelesaian x ≥ 0

 

daerah penyelesaian y > 0

 

Daerah Arsiran  

 

gambar daerah kotor